Menghitung Pangkat Aljabar Suku Dua dengan Segitiga Pascal dan Contohnya (Materi SMP)

Daftar Materi Fisika

• 1. Bilangan Bulat dan Operasi Hitungnya
• 2. Bentuk Pecahan dan Operasi Hitungnya
• 3. Bentuk Aljabar dan Operasi Hitungnya

Advertisement

Baca Juga:

Untuk menghitung hasil pangkat aljabar suku dua bentuk (a + b)c dengan a dan b adalah bilangan bulat dan c bilangan bulat positif salah satu cara termudahnya adalah dengan menggunakan segitiga pascal. Lalu tahukah kalian bagaimana penerapan (aplikasi) atau penggunaan segitiga pascal dalam menghitung pangkat aljabar suku dua tersebut? Untuk mengetahuinya, silahkan kalian simak baik-baik penjelasan berikut ini.

Apa itu Segitiga Pascal?

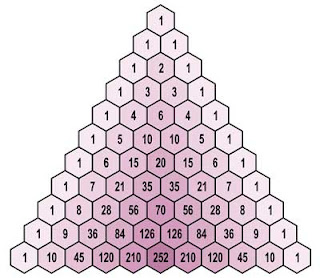
Menurut Wikipedia, segitiga Pascal adalah suatu aturan geometri pada koefisien binomial dalam sebuah segitiga. Bahasa mudahnya adalah seperti ini, segitiga Pascal merupakan barisan angka-angka yang tersusun sedemikian rupa hingga apabila dihubungkan dengan suatu garis pada bagian tepinya akan membentuk bangun segitiga. Perhatikan gambar berikut ini.

Segitiga Pascal ini menyatakan koefisien dari suatu hasil perpangkatan suku dua seperti bentuk (a + b), (x + y), (m + n), (p + q) dan sebagainya. Dari gambar segitiga Pascal di atas, semakin ke bawah deretan angka akan semakin panjang dan nominalnya akan semakin besar. Hal ini selaras dengan nominal pangkatnya.

Bagaimana Cara Membangun Segitiga Pascal?

Barisan segitiga Pascal umumnya dihitung dimulai dengan baris kosong, dan nomor-nomor dalam barisan ganjil biasanya diatur agar terkait dengan nomor-nomor dalam barisan genap. Untuk membuat konstruksi sederhana pada segitiga Pascal dilakukan dengan cara berikut.

□ Di barisan nol, hanya ditulis nomor 1.

□ Kemudian, untuk membangun unsur-unsur barisan barikutnya, tambahkan nomor di atas dan di kiri dengan nomor secara langsung di atas dan di kanan untuk menemukan nilai baru.

□ Jika nomor di kanan atau kiri tidak ada, gantikan suatu kosong pada tempatnya. Misalnya, nomor satu di barisan pertama adalah 0 + 1 = 0, di mana nomor 1 dan 3 dalam barisan ketiga ditambahkan untuk menghasilkan nomor 4 dalam barisan keempat.

Untuk lebih jelasnya, perhatikan ilustrasi pembuatan segitiga Pascal dalam animasi berikut ini.

Cara Menggunakan Segita Pascal

Misalkan kita akan menentukan pola koefisien pada penjabaran bentuk aljabar suku dua (a + b)n, dengan n bilangan asli. Perhatikan uraian berikut.

□ (a + b)1 = a + b → koefisiennya 1  1

□ (a + b)2 = (a + b)(a + b)

= a2 + ab + ab+ b2

= a2 + 2ab+ b2 → koefisiennya 1  2  1

□ (a + b)3 = (a + b)(a + b)2

= (a + b)(a2 + 2ab + b2)

= a3 + 2a2b + ab2 + a2b + 2ab2 + b3

= a3 + 3a2b + 3ab2 + b3 → koefisiennya 1  3  3  1

dan seterusnya.

Adapun pangkat dari a (unsur pertama) pada (a + b)n dimulai dari an kemudian berkurang satu demi satu dan terakhir a1 pada suku ke-n. Sebaliknya, pangkat dari b (unsur kedua) dimulai dengan b1 pada suku ke-2 lalu bertambah satu demi satu dan terakhir bn pada suku ke-(n + 1).

Perhatikan pola koefisien yang terbentuk dari penjabaran bentuk aljabar (a + b)n di atas. Pola koefisien tersebut ditentukan menurut segitiga Pascal berikut.

Pada segitiga Pascal tersebut, bilangan yang berada di bawahnya diperoleh dari penjumlahan bilangan yang berdekatan yang berada di atasnya.

Sekarang coba perhatikan aturan penerapan segitiga Pascal dalam menjabarkan perpangkatan aljabar suku dua berikut ini.

Contoh:

(a + b)5 = 1(a)5(b)0 +  5(a)4(b)1 + 10(a)3(b)2 + 10(a2)(b)3 + 5(a)1(b)4 + 1(a)0(b)5

□ Dari perhitungan di atas, angka bercetak tebal menyatakan koefisien yaitu 1, 5, 10, 10, 5, 1. Hal ini sesuai dengan pola angka pada baris ke-6 segitiga Pascal di atas.

□ Kemudian apabila kalian perhatikan, pangkat variabel a dari kiri ke kanan semakin berkurang yaitu a5, a4, a3, a2, a1 dan a0.

□ Sedangkan pangkat variabel b dari kiri ke kanan semakin bertambah yaitu b0, b1, b2, b3, b4 dan b5.

□ Jadi dapat dikatakan bahwa jumlah pangkat dari a dan b selalu 5 sesuai dengan banyaknya perpangkatan aljabar suku dua tersebut. Perhatikan uraian berikut.

● 1(a)5(b)0 = 5 + 0 = 5

● 5(a)4(b)1 = 4 + 1 = 5

● 10(a)3(b)2 = 3 + 2 = 5

● 5(a)1(b)4 = 1 + 4 = 5

● 1(a)0(b)5 = 0 + 5 = 5

Dari hasil perhitungan di atas, maka hasil dari (a + b)5 adalah sebagai berikut.

(a + b)5 = a5 + 5a4b1 + 10a3b2 + 10a2b3 + 5a1b4 + b5

Contoh Soal dan Pembahasan

Jabarkan perpangkatan bentuk aljabar berikut.

a. (x + 2)2

b. 3(2x – 1)3

c. 2(3p + q)4

d. –3(–x – y)3

e. (4x – 2y)3

f. 5(3a + 2)4

g. (y + 1)5

h. (–2x – 3y)3

Penyelesaian:

a. (x + 2)2 = 1(x)2(2)0 + 2(x)1(2)1 + 1(x)0(2)2

= x2 + 4x + 4

b. 3(2x – 1)3 = 3[1(2x)3(-1)0 + 3(2x)2(-1)1 + 3(2x)1(-1)2 + 1(2x)0(-1)3]

= 3(2x3 – 12x2 + 6x – 1)

= 6x3 – 36x2 + 18x – 3

c. 2(3p + q)4 = 2[1(3p)4(q)0 + 4(3p)3(q)1 + 6(3p)2(q)2 + 4(3p)1(q)3 + 1(3p)0(q)4]

= 2(81p4 + 108p3q + 54p2q2 + 12pq3 + q4)

= 162p4 + 216p3q + 108p2q2 + 24pq3 + 2q4

d. –3(–x – y)3 = -3[1(-x)3(-y)0 + 3(-x)2(-y)1 + 3(-x)1(-y)2 + 1(-x)0(-y)3]

= -3(-x3 – 3x2y – 3xy2 – y3)

= 3x3 + 9x2y + 9xy2 + 3y3

e. (4x – 2y)3 = 1(4x)3(-2y)0 + 3(4x)2(-2y)1 + 3(4x)1(-2y)2 + 1(4x)0(-2y)3

= 64x3 – 96x2y + 48xy2 – 8y3

f. 5(3a + 2)4 = 5[1(3a)4(2)0 + 4(3a)3(2)1 + 6(3a)2(2)2 + 4(3a)1(2)2 + 1(3a)0(2)4]

= 5[1(81a3)(1) + 4(27a3)(2) + 6(9a2)(4) + 4(3a)(4) + 1(1)(16)]

= 5(81a3 + 216a3 + 216a2 + 48a + 16)

= 405a3 + 1080a3 + 1080a2 + 240a + 80

g. (y + 1)5 = 1(y)5(1)0 + 5(y)4(1)1 + 10(y)3(1)2 + 10(y)2(1)3 + 5(y)1(1)4 + 1(y)0(1)5

= y5 + 5y4 + 10y3 + 10y2 + 5y + 1

h. (–2x – 3y)3 = 1(-2x)3(-3y)0 + 3(-2x)2(-3y)1 + 3(-2x)1(-3y)2 + 1(-2x)0(-3y)3

= 1(-8x3)(1) + 3(4x2)(-3y) + 3(-2x)(9y2) + 1(1)(-27y3)

= -8x3 – 36x2y – 54xy2 – 27y3